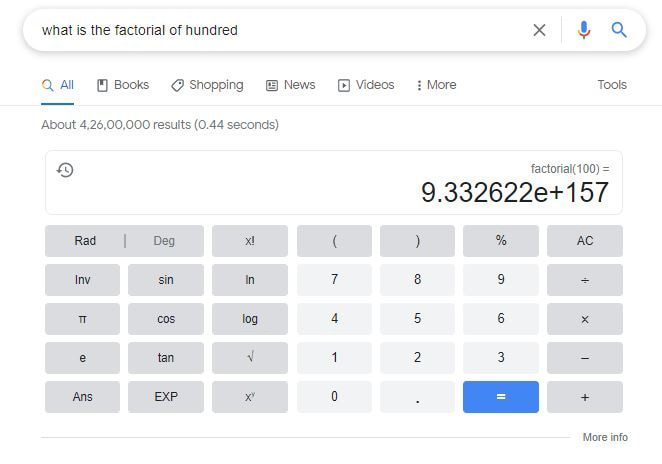
What is the Factorial of one hundred? what is the Factorial of hundred 100 Basically, a Factorial is the product of a positive integer and the Factor of its smaller parts. For example, a three-digit number is the product of a six-digit number and the first seven-digit number. If you shuffle 52 cards and find the Factorial of one hundred, you get a number between one hundred and one thousand.
What is Factorial?
The product of all positive integers less than or equal to a given positive integer, indicated by that integer plus an exclamation point, is known as auctorial in mathematics. As a result, Factorial seven is expressed as 7!, which means 1 2 3 4 5 6 7. The Factorial zero is equal to one. In the evaluation of permutations and combinations, as well as the coefficients of terms in binomial expansions, Factorials are frequently encountered No integral values have been included in Factorials.
Factorials were found by Jewish mystics in the Talmudic book Sefer Yetzirah and by Indian mathematicians in the canonical works of Jain literature. The Factorial operation appears in many fields of mathematics, particularly in combinatorics, where its most fundamental use counts the number of unique sequences – permutations – of n distinct objects: there are n! Factorials are employed in power series for the exponential function and other functions in mathematical analysis, and they can also be found in algebra, number theory, probability theory, and computer science.
More info
Much of the Factorial function’s mathematics was established in the late 18th and early 19th century. Stirling’s approximation approximates the Factorial of huge numbers accurately, demonstrating that it grows faster than exponential growth. Legendre’s formula can be used to count the Factorials’ trailing zeros by describing the exponents of prime numbers in a prime Factorization of the Factorials. The Factorial function was interpolated by Daniel Bernoulli and Leonhard Euler to a continuous function of complex numbers, the gamma function, except for the negative integers.
The Factorials are closely related to many other famous functions and number sequences.
Including binomial coefficients, double Factorials, falling Factorials, primorials, and sub Factorials. Implementations of the Factorial function are used in scientific calculators and scientific computing software libraries and are frequently cited as examples of various computer programming approaches. Although computing big Factorials directly using the product formula or recurrence is inefficient, faster algorithms exist that match the time for fast multiplication procedures for numbers with the same number of digits to within a constant factor.
Factorial of a hundred Meaning
The Factorial of a hundred is the sum of all natural numbers that are smaller than n. In other words, the Factorial of a hundred is the product of all integers that are larger than n. It is the highest power of a digit, followed by the second-highest power. In math, the Factorial of a hundred is a number that is higher than the number it is based on.
The Factorial of a hundred is a product of two digits. For example, a three-digit number is equal to 72 digits. A Factorial of more than one pixel equals the sum of two digits. This is called the product of two digits. The Factorial of a hundred is referred to as the product of four natural numbers. The product of a three-digit number is called a multiplication.
What is the Factorial of 100?
In this article we’ll show you how to calculate the Factorial of 100 with a really quick, step-by-step explanation of how it’s calculated.
First off, what exactly is a Factorial? The Factorial is the result of multiplying all whole numbers in a chosen number (in this case 100) all the way down to 1.
You will generally see Factorials expressed with an exclamation mark after the number, like so:
100!
In this case, the number of whole numbers in 100 is more than five. You can see how this can quickly get out of hand with larger numbers.
Factorials are used in math quite a lot when calculating the number of possible combinations or permeatations of something. If you think about shuffling a deck of 52 cards, you can use Factorials to calculate how many possible orders there are.
When describing a Factorial you would usually say 100! like “100 Factorial”, “100 shriek”, or “100 bang”. Personally, I prefer shriek!
Hopefully this article has helped you in your quest to calculate the Factorial of 100. Feel free to share with your friends, family, teachers, and anybody who might be interested in factorials of numbers (which is surely everyone!).
Factorial of a Hundred Meaning
The Factorial of a hundred is the sum of all natural numbers that are smaller than n. In other words, the Factorial of a hundred is the product of all integers that are larger than n. It is the highest power of a digit, followed by the second-highest power. In math, the Factorial of a hundred is a number that is higher than the number it is based on.
The Factorial of a hundred is a product of two digits. For example, a three-digit number is equal to 72 digits. A Factorial of more than one pixel equals the sum of two digits. This is called the product of two digits. The Factorial of a hundred is referred to as the product of four natural numbers. The product of a three-digit number is called a multiplication.
Factorial of a hundred Definition
The factor of a hundred is the product of all integers less than n. It is a number of three digits that is higher than n. It is called a “high-ranking number” because it is higher than the number it is multiplying. Similarly You can use this number to determine how many digits are in a given amount of space. This is the lowest number you can find.
A Factorial of a hundred is a number of three digits. It is the product of all integers between n and ninety-nine. The Factorial of a hundred equals 193-4-8-5, where the first digit is equal to eight. The second digit, or ten-digit, is equal to the first byte of the Factorial of a hundred.
Types of Multiplication
The Factorial of a number is the product of all the whole numbers less than or equal to that number. Factorial of zero is equal to one, since multiplying a product by zero leaves the root unchanged.
The Factorial of a negative number is undefined. However, When calculating multiples of larger numbers, it can be useful to avoid writing out repeated multiplication (i.e., avoiding calculators or operations which require pencil-and-paper subtraction).
Multiplication is the repeated addition of a certain number by another and factors are what we get when we multiply the same number by itself. Thirdly The term “Factorial” has been in use, in England, to designate any product of consecutive integers which may be positive or negative.
Types of Factorials
A Factorial is the product of all integers that precede it. This can be a difficult concept to understand, and so division will be shown. Similarly The Factorial of four is twenty-four because four multiplied by three multiplied by two multiplied by one is 24. But Three multiplied thirteen times would equal 39924 or one hundred times fourteenth power. A Factorial equals x(x-1)(x-2)…(1).
Some people might think that it would take forever to calculate the Factorial of 100 and the answer is, fortunately, 22! But how do you get there? If we think about what x equals in our equation, it’s going to be 100. We can then cross-multiply and have 100*99*98*97*96…until we get 1. Then we just multiply them together or just add all those numbers together! In mathematics, 5! is defined as 5*4*3*2*1.
In this example, the Factorial of 5 would be 3120.
| Please, enter a natural number between 0 and 10,000:
f |
How to calculate the Factorial of 100Detailed answer
100! = 100 • 99 • 98 • 97 • 96 … 3 • 2 • 1 |
Also Read :Will Smith and Chris Rock Oscars 2022 Incident Over Jada Pinkett Smith
Here you can find answers to questions like: What is the Factor of 100? What is the Factal of 100? What are the last digits of Factor of 100? How many trailing zeros in 100 Factor? How many digits are there in 100 Factor? Use the Factorial calculator above to find the factor of any natural between 0 and 10,000.
What is Factorial?
Definition of Factorial
Firstly The Factorial is a quantity defined for any integer n greater than or equal to 0.
The factor is the product of all integers less than or equal to n but greater than or equal to 1. factor value of 0 is by definition equal to 1. For negative integers, factorials are not defined. Factorial can be seen as the result of multiplying a sequence of descending natural numbers (such as 3 × 2 × 1).
The factorial symbol is the exclamation mark !.
The factorial formula
If n is a natural number greater than or equal to 1, then
n! = n x (n – 1) x (n – 2) x (n – 3) … 3 x 2 x 1
If n = 0, then n! = 1, by convention.
Example: 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720
In the other words, the Factor of one hundred is the product of an integer that is positive. Secondly A factor of six is that it is the product of all its smaller components. For example, if the three-digit number has the same number as the first seven-digit number it’s a Factorial of seventy-eight. This simple calculation will give you the numbers that is between one and one hundred.
This mathematical formula can be useful to determine the worth of a certain product.
The Factor of 100 contains 158 digits with twenty-four zeros near the top. A Factorial of one hundred is the result of a number having an positive number. A of one thousand is composed of three digits and four digits. With a calculator, a hundred is simple to calculate. If you’re in need of more sophisticated methods, you might want to consider the Factorial course.
Also Read: People Share Photos Of Sleeping Puppies In A Strange Position
Definitions of Factorial
Here are some definitions of Factorial
- It is the product of its Factors.
- The product of the natural numbers from 1 to n.
- Factorial of n is defined as the product of all positive integers from 1 to n.
- As the number of possible outcomes of an event or situation
What is Sub Factorial of a Number?
A mathematical term “sub-Factorial”, defined by the term “!n”, is defined as the number of rearrangements of n objects. It means that the number of permutations of n objects so that no object stands in its original position. The formula to calculate the sub-Factorial of a number is given by:
Factorial of 5
Finding the Factorial of 5 is quite simple and easy. This can be found using formula and expansion of numbers. This is given below with detailed steps.
We know that,
n! = 1 × 2 × 3 …… × n
Factorial of 5 can be calculated as:
5! = 1 × 2 × 3 × 4 × 5
5! = 120
Therefore, the value of factorial of 5 is 120.
Explanation The Factorial of a Hundred
The factor of a hundred is the product of three digits. Its meaning is that it is the number of digits with the highest power of n. However, The product of two digits is called the of a hundred. For Instance, If a number has two lower digits. For Instance, So its is the sum of both lower numbest. This way, the of a hundred is 100 times bigger than the sum of two other numbers.
The factor of a hundred is a product of positive integers. For instance, if the number is 10, After that it is ten times the product of ten. Similarly, of a hundred is ten times the product of one positive digit. Because Its length is two hundred and twenty-four trailing zeros. Then, it is the product of a hundred. The number 100 is the same as a whole-digit number.
Factorial of 100- Applications of Factorial
The Factorl function was first used to count permutations: So there are n! different ways to arrange n different objects into a series. Factorls are used more widely in combinatorics formulas to account for different object orderings. The binomial coefficients (n k), for example, count the k-element combinations (subsets of k elements) from a collection of n elements and can be obtained using Factorls. The Factorials are added to the Stirling numbers of the first kind, So the permutations of n are counted in subsets with the same number of cycles. Counting derangements. For Instance, permutations that do not leave any element in its original location, is another combinatorial application; Similarly the number of derangements of n items equals the nearest integer to n! / e.
The binomial theorem, which employs binomial coefficients to expand powers of sums. Moreover, gives rise to Factorials in mathematics. They can also be found in the coefficients that are used to connect specific families of polynomials, such as Newton’s identities for symmetric polynomials. Because The Factorials are the orders of finite symmetric groups, which explains their application in counting permutations algebraically. Factorials appear in Faà di Bruno’s formula for chaining higher derivatives in calculus. Factorials regularly appear in the denominators of power series in mathematical analysis, most notably in the series for the exponential function.
Factorial Tables Chart 1! to 51! |
|---|
| 1 = 1 |
| 2 = 2 |
| 3 = 6 |
| 4 = 24 |
| 5 = 120 |
| 6 = 720 |
| 7 = 5040 |
| 8 = 40320 |
| 9 = 362880 |
| 10 = 3628800 |
| 11 = 39916800 |
| 12 = 479001600 |
| 13 = 6227020800 |
| 14 = 87178291200 |
| 15 = 1307674368000 |
| 16 = 20922789888000 |
| 17 = 355687428096000 |
| 18 = 6402373705728000 |
| 19 = 121645100408832000 |
| 20 = 2432902008176640000 |
| 21 = 51090942171709440000 |
| 22 = 1124000727777607680000 |
| 23 = 25852016738884976640000 |
| 24 = 620448401733239439360000 |
| 25 = 15511210043330985984000000 |
| 26 = 403291461126605635584000000 |
| 27 = 10888869450418352160768000000 |
| 28 = 304888344611713860501504000000 |
| 29 = 8841761993739701954543616000000 |
| 30 = 265252859812191058636308480000000 |
| 31 = 8222838654177922817725562880000000 |
| 32 = 263130836933693530167218012160000000 |
33 = 8683317618811886495518194401280000000 |
| 34 = 295232799039604140847618609643520000000 |
| 35 = 10333147966386144929666651337523200000000 |
| 36 = 371993326789901217467999448150835200000000 |
| 37 = 13763753091226345046315979581580902400000000 |
| 38 = 523022617466601111760007224100074291200000000 |
| 39 = 20397882081197443358640281739902897356800000000 |
| 40 = 815915283247897734345611269596115894272000000000 |
| 41 = 33452526613163807108170062053440751665152000000000 |
| 42 = 1405006117752879898543142606244511569936384000000000 |
| 43 = 60415263063373835637355132068513997507264512000000000 |
| 44 = 2658271574788448768043625811014615890319638528000000000 |
| 45 = 119622220865480194561963161495657715064383733760000000000 |
| 46 = 5502622159812088949850305428800254892961651752960000000000 |
| 47 = 258623241511168180642964355153611979969197632389120000000000 |
| 48 = 12413915592536072670862289047373375038521486354677760000000000 |
| 49 = 608281864034267560872252163321295376887552831379210240000000000 |
| 50 = 30414093201713378043612608166064768844377641568960512000000000000 |
51 = 1551118753287382280224243016469303211063259720016986112000000000000 |
How do I find the result of two Factorials?
The term “Factorial” refers to an infinity number. It is the most powerful for any number with three digits. The sum of numbers that are between 100 and 99999. So It also represents the number of numbers in the range 100 to 200. Also, it is the least number of two-digit numbers. Therefore the Factorial of a hundred is an extremely beneficial tool in myriad math-related applications. It is crucial in the calculation of probabilities, statistics, as well as graphs.
If you multiply a number by the number. Second natural numbers are the exact same as the two previous ones. So, the Factorial of 100 is nineteen-three-four-eight-five. Therefore, the end outcome of the Factorial will be eight. Furthermore the product with ten digits is identical to the second digit.
How much is 100 Factorial?
The answer of what is the Factorial of 100 The number of digits in 100 factorial is 158.
How many digits is 100 factorial?
158 digits Factorial of 100 has 158 digits. It is impossible to save a lot of these digits even if we use long long int. The following is a simple solution where we use an array to store the digits of each results. The idea is to use basic mathematics for multiplication.
How do you find 99 Factorial?
Factorial number is the product of all the integers from 1 to that number. For example, Factorial of 6 is 1*2*3*4*5*6 = 720.
How do you calculate Factorials?
To find the Factorial of a number, multiply the number with the factorial value of the previous number. For example, to find out the value of 6! Multiply 120 (the factorial of 5) by 6, and get 720.
How do you find the Factorial of 100 in C?
How to calculate 100 factorial (100!) in C. 0916864000000000000000000000000 which is 158 digits long and the maximum value of unsigned long long int in C is 18,446,744,073,709,551,615.
How much is 100 Factorial?
The answer of what is the Factorial of 100 The number of digits in 100 factorial is 158.
How many digits is 100 factorial?
158 digits Factorial of 100 has 158 digits. It is impossible to save a lot of these digits even if we use long long int. The following is a simple solution where we use an array to store the digits of each results. The idea is to use basic mathematics for multiplication.
How do you find 99 Factorial?
Factorial number is the product of all the integers from 1 to that number. For example, Factorial of 6 is 1*2*3*4*5*6 = 720.
How do you calculate Factorials?
To find the Factorial of a number, multiply the number with the factorial value of the previous number. For example, to find out the value of 6! Multiply 120 (the factorial of 5) by 6, and get 720.
How do you find the Factorial of 100 in C?
How to calculate 100 factorial (100!) in C. 0916864000000000000000000000000 which is 158 digits long and the maximum value of unsigned long long int in C is 18,446,744,073,709,551,615.






